【數碼金魚缸】筆者過去研究使用量化模型選股,最終目的是要透過買入一籃子「瘦身偏右」的股票,砌出「勇武」與「和理非」並重的「均衡組合」。這次將會研究如何使用更聰明的「機器學習」算法,快速和有效率地進行優化(optimization),以便應用到資訊量巨大的金融市場上。
一個投資組合可定義為X=【X1, X2, X3……Xn】,個別X值代表每隻股票的比重。另外,定義一組目標函數y=f(X),用來衡量某個X投資組合的表現,例如使用組合夏普比率作為目標函數。所謂的optimization,就是透過各種算法,找出能夠最小化(或最大化)目標函數輸出的一組X值的過程。
由於X是一支由n個數字組成的向量(vector),它的變化理論上是無窮無盡的。舉例說,一個30隻股票的投資組合,如果限制個股倉位只能是0或1/30,則所有可能性為2的30次方,總量已高達約10.7億次。這對於普通一台家用電腦而言,如要測試所有可能性去找最佳X值,已有點吃力。如股票數量再增加,且每隻股票比重是連續的可變數,可能性總量更是天文數字。
因此筆者於上一篇稿否決了蠻力算法(brute-force)的可能性,進而嘗試使用隨機抽樣方式,希望透過大量隨機抽樣撞中接近優化組合;結果雖然不完美,但可接受,當然也有很大改進空間。除了速度慢,隨機抽樣方法也不保證可找到最優化組合,一切仍視乎運氣。
藉爬山算法快速到山頂
筆者使用Python模組scipy.optimize當中一個名為minimize的功能,這裏給它起個易記的名稱叫作「爬山算法」。讀者可以把所有的X值可能性想像成一座大山,山頂或山谷代表最優化的投資組合。如果使用蠻力算法,好比跑完每一條可行的路線,才找到哪個是山頂。而隨機算法則好比隨機選出部份登山路線,希望其中一條能夠登頂。這次我們使用的爬山算法,可以快速找出路線到達山頂(或山谷)。
爬山算法主要是運用了數學上partial derivatives概念,或在機器學習的範籌稱為gradient descent,原理也是類同。爬山算法透過微調個別X值,觀測它對於目標函數輸出值的影響是否有所優化,並以此作為依據,決定下一步微調的方向和力度,直至微調所有個別的X值也不能導致輸出結果優化時,便可宣告成功找到最佳X值。
就如現實爬山一樣,當手上沒有地圖,也看不到山頂在哪裏,光線只足夠看清方圓一米內的地方,只要每一步也向着陡峭的方向爬,不斷重覆,直至發現所有方位也是平的,你便身處山頂了。這種算法對比蠻力或隨機算法也來得聰明和省力。

設約束確保組合可操作
通常在optimization問題上,也會設下不同的約束(constrains),防止算法在尋找最佳值時變得天馬行空。若不設任何約束,算法便會於負無限大與正無限大之間的任何區域當中搜尋優化X值;儘管這樣找出來的結果在數學上是優化的,但實際上或不能操作。
筆者只設定了兩個約束。約束一:把【X1, X2, X3……Xn】的總和約束為1,意味這是一種典型的長倉策略,算法必須百分百把資金分佈於不同股票上,不保留現金。約束二:規定每個個別X值的區間位於0至w之間,而w是單一股票的比重上限。如設定w值為0.2,算法最少也會選擇五隻或以上的股票,否則將會違反總和為1的約束。然而,如果w值太接近1,算法可能給出高度集中的投資建議。現實操作上,這樣做沒有足夠分散風險,因此筆者建議w值上限不高於0.2。
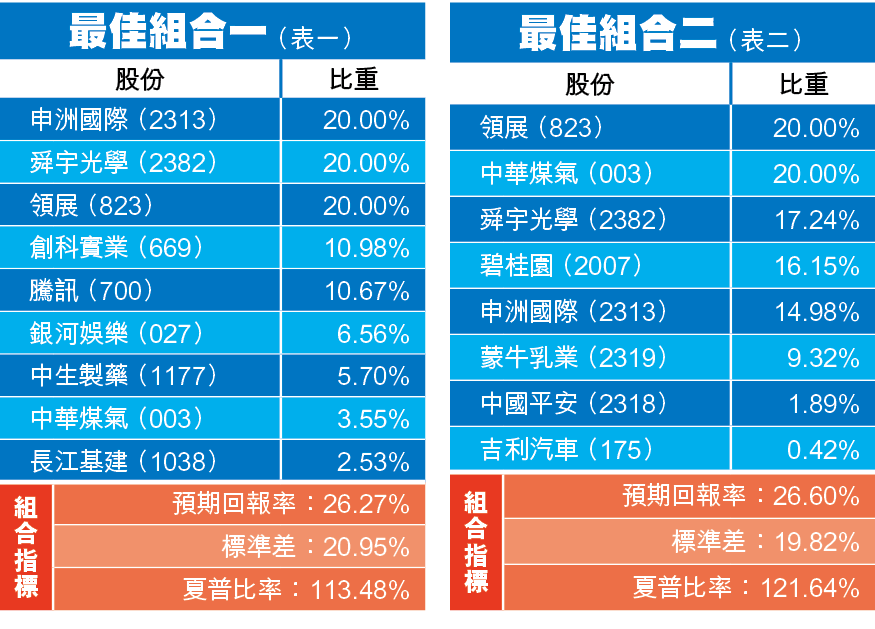
基於以上設定,筆者的爬山算法在恒指成份股內嘗試找出優化組合,以2010年以來數據測試,結果見表1。爬山算法找出的優化組合,對比上一篇稿用隨機程式找出來的組合差別不大,首五大持股當中有四隻是持有相同股票。由於上一篇稿的隨機算法依靠運氣成功找到接近優化的組合,夏普比率優化程度不明顯,只輕微由113.3%提升至113.48%。
爬山算法打敗隨機算法
我們再測試2016年以來的數據,結果見表2。這次的優化組合相對上一篇稿找到的隨機組合有較大的差別,這次的預期回報率和標準差也分別下降了;但由於標準差降低的幅度較大,使夏普比率由113.5%提升至121.64%。這代表使用爬山算法成功找到比隨機算法更有效率的投資組合。
筆者的經驗是,使用爬山算法在任何情況下,也能找到比隨機算法更好的結果。讀者如果有興趣可自行下載筆者編寫的程式進行實驗*。
量子雪球
作者電郵:mailto:[email protected]
*Github link: https://bit.ly/2Nzj4E1