【科健籽:趣味科普】
俗語云:「執輸行頭慘過敗家」,但科學家近年發現,人善人欺天不欺這句老話才是做人的至理。當然在博弈理論預測中,人們往往會放棄雙贏方案,私利行頭,最終變成雙輸的局面。在經典的「囚徒困局」(Prisoner's Dilemma)處境中,就預測大難臨頭各自飛,背叛對方為上上之策。
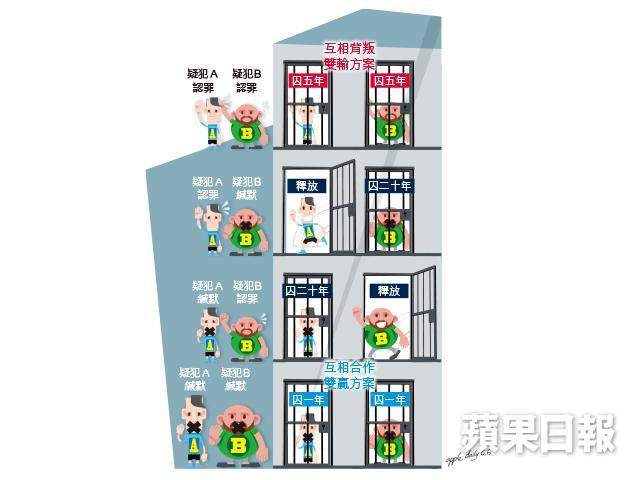
在這個模擬的情境裏,疑犯A和疑犯B兩人均牽涉一單大案,由於警方缺乏足夠證據起訴兩人,因此把二人分開盤問,並開出認罪條件:若一方背信棄義先認罪,然後指證對方,均可以不用坐監即時離去;如兩人都不招供,則一起坐一年;若雙方同時認罪的話,則齊齊坐五年,但假使一方保持緘默,則要坐二十年之多。本來雙方合作,保持緘默,每人充其量都只是坐一年光景,是雙贏方案;然而在互相猜忌缺乏互信(根本也沒有溝通的機會,建立不了互信),兩人只以自己為出發點,都會指證對方,因為在權衡輕重之下,認罪頂多坐五年,不認雖有坐一年的可能性,但若單方面保持緘默,難保對方不指證自己而要背負坐廿年監的風險,所以說背叛同伴才是最有利的策略,也是著名博弈理論中的納殊均衡點(Nash Equilibrium)所指之處,納殊均衡點由一星期前不幸車禍喪生的諾貝爾經濟學家John Nash提出,凸顯出由個體利益為出發點的結果跟整體的利益往往並非一致。
然而在現實世界中玩「囚徒」遊戲,人們不一定會背叛對方,有實驗就安排四十人在電腦前,跟陌生對手博弈。結果顯示,雖部份人只顧自己不合作,但合作至少一次以上的參加者卻竟佔了大多數,他們不一定採取背叛的策略。兩年前,科學家甚至在女子監獄進行實驗,把女囚犯和學生分組進行「囚徒困局」 遊戲並作出比較,遊戲的獎品當然並非減刑,而是以煙仔咖啡(囚犯)和歐元(學生)為誘。結果顯示,囚犯並非如簡單博弈理論所預測般都背叛對方。事實上,他們甚至比學生組背叛得更少。在37%的遊戲中,學生都合作達到雙贏,囚犯的合作比率甚至高達56%之多。

自私精終被孤立
當然,如果多了自由配的元素,則自私的人往往是輸家。在一個多達八百人的複雜網絡實驗中,參加遊戲的人可以自由配對,隨意找尋對手,每位玩家開始時都有相同的點數,他們可以選擇給五十點給對方,或是自私一點留給自己,每一個單元的遊戲結束後都容許當中三分一的參加者更換對手,科學家發現,可換對手的會選擇跟付出的人玩,而自私的玩家通常會給孤立起來,最後這一批「不合作」的玩家就會痛改前非,不再自私。這個實驗說明,若果你讓人們自己建立社交網絡,他們都會傾向尋找付出的人合作,只要避免誤信奸人而受騙,好人也有出頭天。
參考資料:
"Dynamic social networks promote cooperation in experiments with humans." Proceedings of the National Academy of Sciences. 2011 Nov 29; 108(48): 19193–19198.
"Prisoners and their dilemma." Journal of Economic Behavior & Organization, Volume 92, August 2013, Pages 163–175
記者:陳以恒
編輯:黃仲兒
美術:楊永昌